Code

The code for most papers is available on Github.

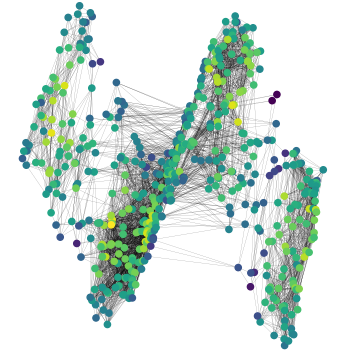
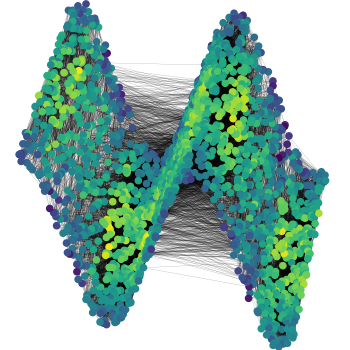
Convergence and stability of GNNs on large random graphs

Here.

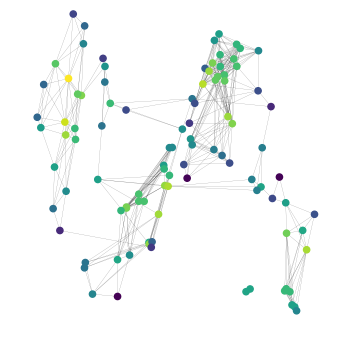
NEWMA: Scalable model-free online change-point detection

The code for this paper is available here.

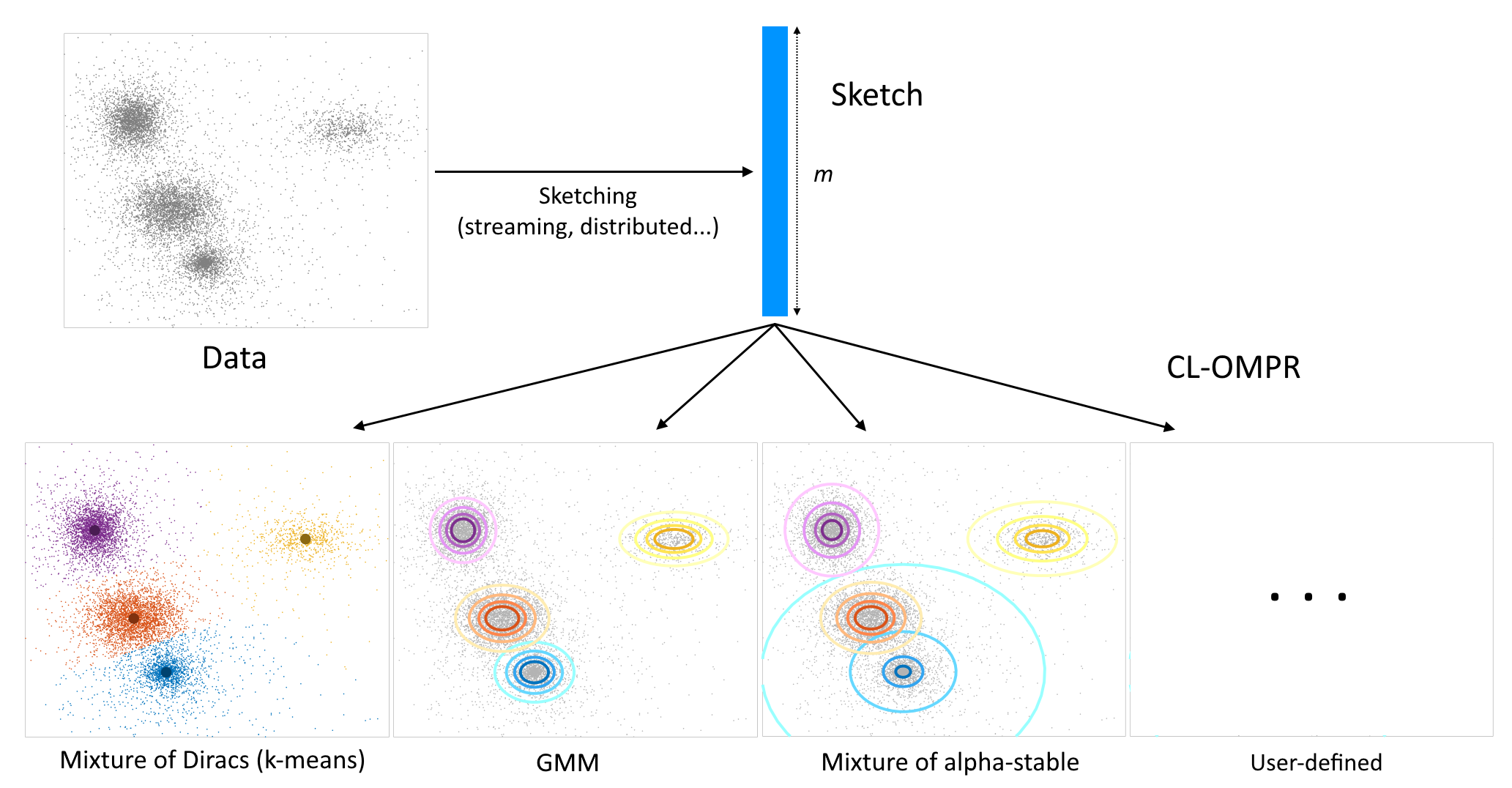
Sketched Mixture Model Learning: SketchMLbox

Linear sketches are a general class of compressed representations of databases (this book is a great reference), such that: the sketch of the union of two databases is the sum of their sketches. This includes histograms or hash tables. A typical “sketched” method has two steps: a compression step, to compute the sketch, and a learning step, to extract relevant information from the sketch. Linear sketches are built such that the compression step is amenable to streaming, distributed or parallel computing. Then, learning from the sketch is usually inexpensive compared to learning directly from raw data.

The SketchMLbox is a Matlab toolbox for unsupervised mixture model estimation from a sketch: it handles Gaussian Mixture Models, but also mixture of Diracs (sketched k-means) or mixture of alpha-stable distributions. It is optimized so that users can implement their own models. Its core is the Compressed Learning Orthogonal Matching Pursuit with Replacement (CL-OMPR) algorithm, a greedy heuristic for sketched mixture model estimation. It also implements a particular sketching method that uses Random Fourier Features (with functionalities to select the best distribution of frequencies, etc.), but can be adapted to any sketch.

The code can be found here. For applications and theoretical guarantees, see our publications. Feedback is always valued, if you have questions send me a mail.

Source Separation with mixture of alpha-stable distributions

Gaussian Mixture Models can be used to assign time-frequency bins of a spectrogram to different sources, and separating them. In this paper, we use the CL-OMPR algorithm to learn an exotic mixture model specially designed for this case: each component is the sum of an alpha-stable distribution with rank-one precision matrix (which represents the steering vector, or “direction” of the source), and Gaussian noise. The code is available on my Github.